Trong toán học hình học bậc trung học phổ thông, hình chóp không còn xa lạ gì đối với các bạn. Thế nhưng một hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng thì bạn có biết không? Bài viết này sẽ trả lời giúp bạn câu hỏi và sẽ cung cấp một số điều về hình chóp tứ giác đều. Bên cạnh đó, chúng tôi sẽ giúp bạn giải một số bài toán liên quan đến hình chóp tứ giác đều và một số lưu ý khi bạn làm bài tập. Để có thể giải toán một cách dễ dàng, nhìn hình học không gian một cách đơn giản hơn thì hãy theo dõi bài viết này nhé. Hi vọng sau khi đọc xong bài này các bạn có thể nắm vững kiến thức về hình học không gian hơn. Và mong đây sẽ là bài viết dùng để tham khảo phù hợp với học sinh, phụ huynh lẫn thầy cô giáo.
Bạn có biết hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng
Hình chóp không chỉ xuất hiện trong toán học mà nó xuất hiện rất nhiều ngoài cuộc sống. Ví dụ như kim tự tháp là một hình chóp tứ giác đều. Vậy bạn có thể trả lời được kim tự tháp có bao nhiêu mặt phẳng đối xứng không? Trả lời cho bạn biết đó là, hình chóp tứ giác đều gồm có 4 mặt phẳng đối xứng. Để trả lời được câu hỏi này, chúng ta phải biết được mặt phẳng đối xứng là như thế nào. Sau đó vẽ hình chóp tứ giác đều để kiểm tra xem có bao nhiêu mặt phẳng thỏa mãn điều này. Trước tiên, mặt phẳng đối xứng chúng ta có thể hiểu đó là: Cho một khối (A), nếu thực hiện phép đối xứng qua mặt phẳng (I) thì biến (A) thành chính nó. Khi đó ta nói mặt phẳng (I) chính là mặt phẳng đối xứng của khối hình học (A). Như vậy, hình chóp tứ giác đều sẽ có 4 mặt phẳng đối xứng trong đó có 2 mặt phẳng nối từ đỉnh đến hai đường chéo và 2 mặt phẳng nối từ đỉnh chóp đến trung điểm của các cặp cạnh đối.
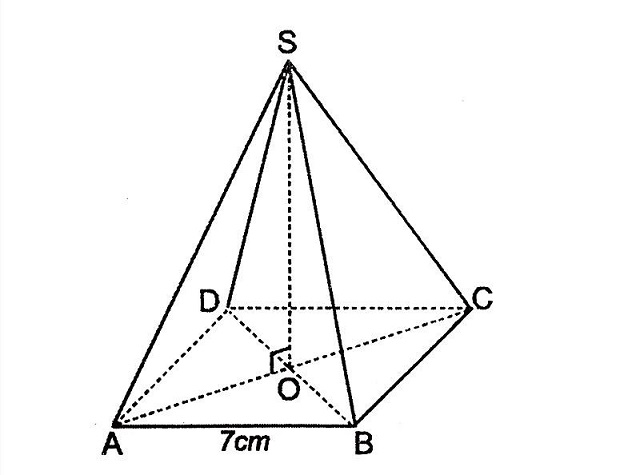
Một số điều về hình chóp tứ giác đều mà bạn có thể chưa biết
Hình chóp trong hình học không gian có rất nhiều loại. Để gọi là hình chóp thì phải có đáy là đa giác và các mặt bên là các tam giác có chung một đỉnh. Hình chóp đều là hình chóp mà mặt đáy là đa giác đều ( có thể là tam giác đều, hình vuông, lục giác đều,….). Và các mặt bên là các tam giác cân tại đỉnh, các tam giác bằng nhau và có chung đỉnh. Như vậy hình chóp tứ giác đều sẽ có tính chất đó là: Đáy là hình vuông, các cạnh bên bằng nhau, các mặt là các tam giác bằng nhau và cân tại đỉnh. Các góc tạo bởi cạnh bên và mặt đáy cũng bằng nhau. Thể tích hình chóp tứ giác đều sẽ bằng 1/3 tích diện tích đáy nhân với chiều cao của hình chóp.
Giúp bạn giải một số bài toán về hình chóp tứ giác đều
Sau khi có thể trả lời câu hỏi về hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ở phần trên. Thì bây giờ để nắm vững phần lý thuyết chúng tôi sẽ cung cấp cho bạn một số bài tập liên quan đến hình chóp.
Bài 1: Cho một hình chóp S. MNO là hình chóp tam giác đều cạnh đáy là h, cạnh bên là 2h. Đề ra: Bạn hãy chứng minh chân đường cao kẻ từ đỉnh S của hình chóp S.MNO là tâm của tam giác MNO. Và tính thể tích của hình chóp tam giác đều S.MNO.
Giải: đầu tiên dựng một đường SH vuông góc với tam giác MNO, ta có: SM=SN=SO nên HM=HN=HO. Vậy ta có H là tâm của tam giác MNO đều ( điều phải chứng minh)
Tính thể tích hình chóp tam giác đều S.MNO: V = 1/3 SMNO * SH
Ta tính được: SH = b√11/√3
Vậy thể tích của hình chóp là b3* √11/12
Bài 2: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 6 cm, đường cao bằng 12 cm. Tính thể tích của hình chóp S.ABCD
Giải: Thể tích hình chóp S.ABCD là: VS.ABCD = 1/3 * đường cao * SABDC
Ta tính được: SABCD= 12*12 = 144 (cm2)
Vậy thể tính của hình chóp S.ABDC là : V = 1/3*6*144 = 288 (cm3)
Trên đây là hai dạng bài tập thường gặp khi học hình học không gian về hình chóp. Bên cạnh những bài tập về hình chóp thì còn có rất nhiều dạng như tính thể tích của hình chóp cụt (tức là hình bị mất phần chóp). Về dạng bài toán này, bạn có thể chia bài toán thành hai phần, phần đầu tiên tính thể tích hình chóp hoàn chỉnh. Phần thứ hai tính thể tích phần hình chóp bị mất. Sau đó lấy phần hoàn chỉnh trừ đi phần bị mất, khi đó bạn sẽ giải ra được kết quả. Để có thể có nhiều bài tập hơn nữa về hình chóp hãy đọc các bài viết khác trên trang web này nhé.
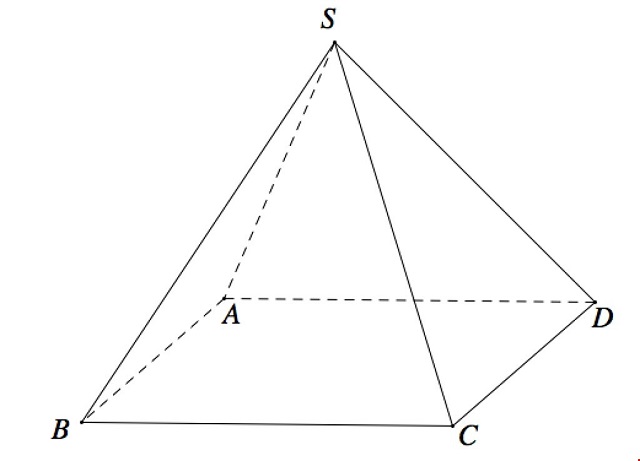
Một số lưu ý khi bạn làm bài tập hình học không gian về tứ giác đều
Để các bạn có thể lấy được điểm trọn vẹn khi làm bài toán hình học không gian, chúng tôi sẽ đưa ra cho bạn một số lời khuyên hữu ích khi làm bài tập. Điều đầu tiên, để làm tốt bài tập thì bạn nên nắm vững lý thuyết. Thật ra toán học rất dễ đối với siêng năng phần lớn bài tập đều lấy từ các phần lý thuyết đã học. Thứ hai, đó là bạn phải đọc thật kỹ đều bài đã ra, đọc kỹ đề phân tích đề chính xác thì khi đó bạn mới có hướng đi đúng đắn cho bài toán. Thứ 3, hình học không gian yêu cầu bạn vẽ hình phải thật chính xác và dễ nhìn. Phần hình cũng là một phần tính điểm trong bài thi nên bạn không bỏ qua điểm số này dù không nhiều. Và khi vẽ hình đúng thì bạn mới có thể phát hiện được các bước mình cần chứng minh. Hoặc khi làm bài trắc nghiệm bạn có thể nhìn vào hình để đoán được đáp án mình sẽ chọn là gì ? Trong trường hợp, bạn không thể tính ra được đáp án. Và điều cuối cùng đó là để làm thật tốt thật nhanh một bài toán hình học không gian, bạn nên làm đi làm lại thật nhiều các dạng toán khác nhau. Khi đó, gặp một bài toán nào đó, bạn sẽ dễ hình dung ra, các bước khi làm dạng này là như thế nào. Tránh trường hợp thử nhiều cách nhưng cuối cùng không có cách nào phù hợp.
Cuối cùng, câu trả lời của câu hỏi : hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng cũng đã được giải đáp. Những điều về hình chóp tứ giác đều cũng đã được cung cấp ở trên. Bên cạnh đó, giúp bạn có thể làm tốt các bài toán về hình chóp thì chúng tôi cũng đưa ra cho bạn những lưu ý mà bạn không nên bỏ qua. Thêm một điều nữa, để đạt điểm tối đa trong môn toán bạn hãy làm hết tất cả các bài toán, chỉ cần phát hiện ra cách làm, hãy tận dụng thời gian để làm hết. Khi chấm điểm cô thầy không chấm theo kết quả mà sẽ chấm theo các bước làm bài. Vì thế dù kết quả sai, thì bạn vẫn có cơ hội được điểm cao. Qua bài viết này thì bạn đã có thể hiểu hơn về hình chóp tứ giác đều rồi chứ. Sau khi đọc xong hãy để lại lời nhận xét của mình dưới bài viết này nhé !
